philosophy
Biological and social systems are differentiated, multipartite, integrated, and dynamic. Data about these systems, now available on unprecedented scales, are often schematized as networks.
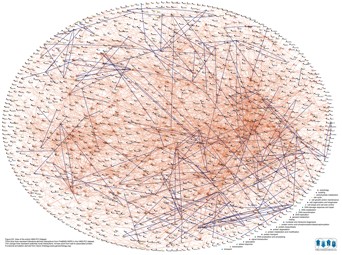
Yeast protein interaction network. Bader and Hogue (2002) Nature
Such abstractions are powerful, but even as abstractions they remain highly complex. Trying to understand a complicated system using a full network diagram is like trying to get from Logan airport to Harvard Square using the following image on the left.
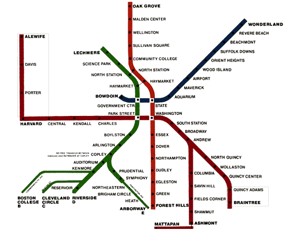
What we really need is the image on the right. We need a good representation that both simplifies and highlights the underlying structures and the relationships in our network; we need a way to make complex networks into useful maps. Our approach is to use information theory to measure how efficiently a map represents the underlying geography. Thus we can quantify and resolve the tradeoff that faces every cartographer: the tradeoff between omitting important structures by oversimplification, and obscuring significant relationships in a barrage of superfluous detail.
method
We map large networks by decomposing the myriad nodes and links into modules or communities, and then identifying the patterns of flow between these modules. Our approach originates within coding theory; we aim to design a code that provides a compressed description of the information flow on the network.
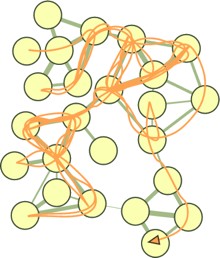
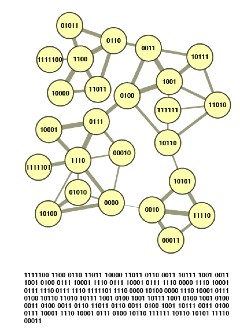 Suppose want to describe the trajectory of this or any other random walk on the network, such that important structures have unique names.
A basic approach is to give a unique name to every node in the network. The Huffman code illustrated here is an efficient way to do so.
Suppose want to describe the trajectory of this or any other random walk on the network, such that important structures have unique names.
A basic approach is to give a unique name to every node in the network. The Huffman code illustrated here is an efficient way to do so.
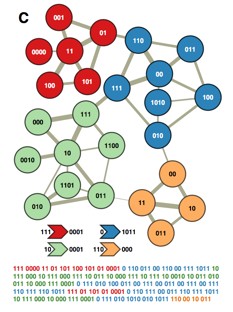
 A two-level description of the random walk, in which major clusters receive unique names but the names of nodes within clusters are reused, yields on average a 32% shorter description for this network. Module codes and exit codes are shown left and right of the arrows under the network.
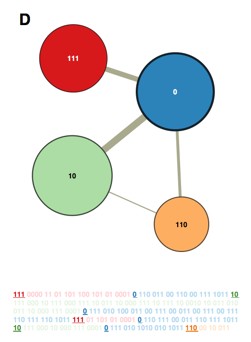
Reporting only the module names, and not the locations within the modules, provides an optimal coarse-graining of the network. This gives us our modular description of the network, and serves as our map.
A two-level description of the random walk, in which major clusters receive unique names but the names of nodes within clusters are reused, yields on average a 32% shorter description for this network. Module codes and exit codes are shown left and right of the arrows under the network.
Reporting only the module names, and not the locations within the modules, provides an optimal coarse-graining of the network. This gives us our modular description of the network, and serves as our map.
further detail
We present the method in full detail in
Rosvall and Bergstrom (2008) and in Rosvall et al. (2010).
An interactive demonstration of the method is available at mapequation.org.
